Rescue-Prime Hash Function
Contents
Rescue-Prime Hash Function#
Important
Rescue-Prime is an arithmetization-oriented hash function, meaning that it has a compact description in terms of AIR.
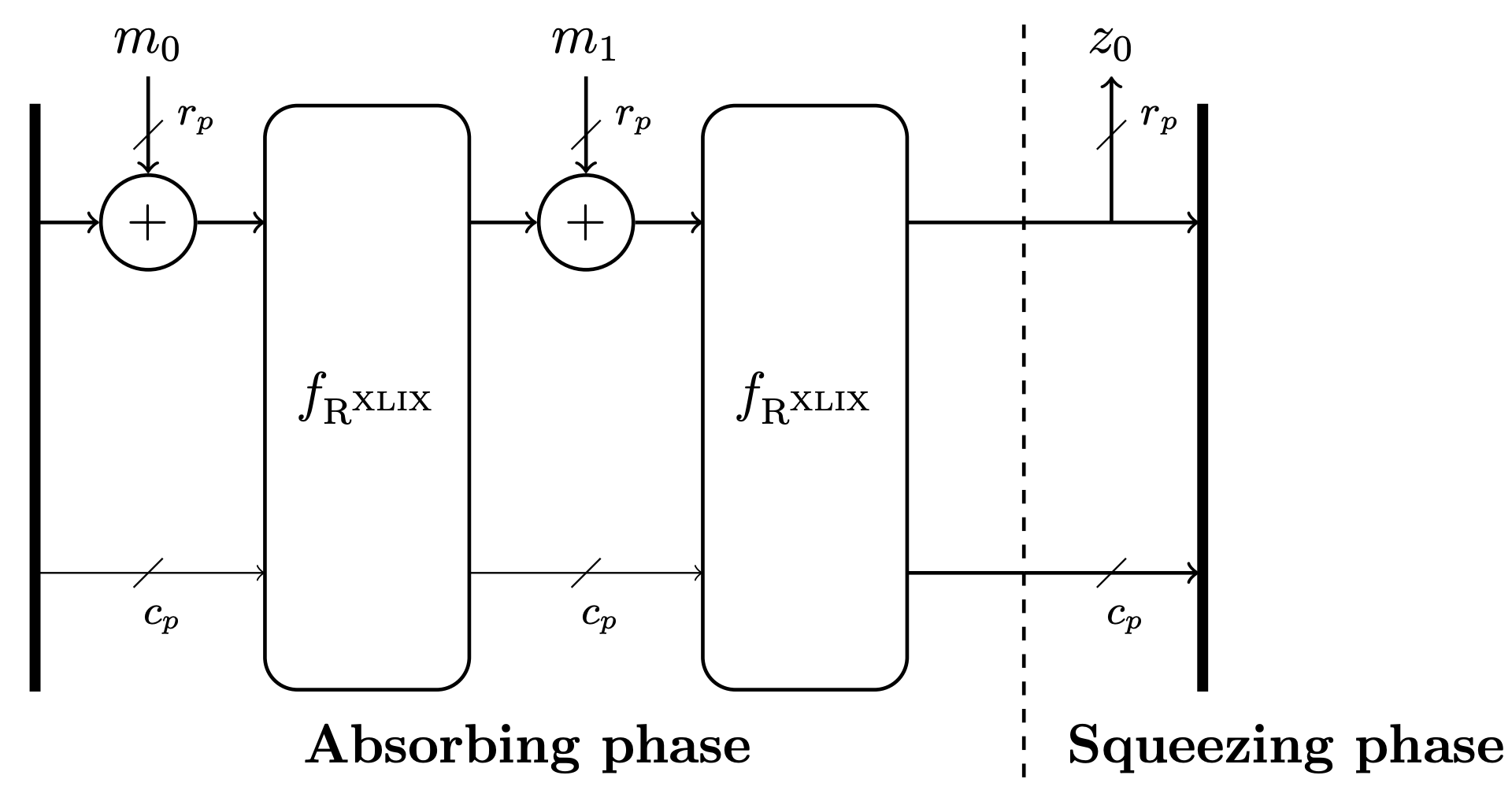
Fig. 1 The Rescue-Prime hash function with two absorbing iterations.#
In the absorbing phase, the following iteration is repeated: the next \(r_{p}\) elements from the input sequence are added to the \(r_{p}\) top elements of the state, after which the permutation \(f_{\mathrm{R}^{\text {XLIX }}}\) is applied to the state. This loop runs until all the input elements have been absorbed.
In the squeezing phase, the top \(r_{p}\) elements of the state are output. In theory, the permutation \(f_{\mathrm{R}^{\text {XLIX }}}\) can be applied to the state iteratively to produce an arbitrarily long sequence of output elements. However, this specification restricts the number of output elements to at most \(r_{p}\).
The Rescue-XLIX Permutation#
The Rescue-XLIX permutation \(f_{R^{\text{XLIX}}}\) consists of \(N\) iterations of the Rescue-XLIX round function.
A single round consists of the following components:
Forward S-box layer: apply the power map \((\cdot)^{\alpha}\) to each element of the state.
Linear layer: apply the MDS matrix to the state, through matrix-vector multiplication.
Round Constants injection: add the next pre-defined \(m\) constants from the list of round constants \(\left\{C_{i}\right\}_{i=0}^{2 m N-1}\) into the state.
Inverse (Backward) S-box layer: apply the inverse power map \((\cdot)^{\alpha^{-1}}\) to each element of the state.
Linear layer: apply the MDS matrix to the state, through matrix-vector multiplication.
Round Constants injection: add the next pre-defined \(m\) constants from the list of round constants \(\left\{C_{i}\right\}_{i=0}^{2 m N-1}\) into the state.
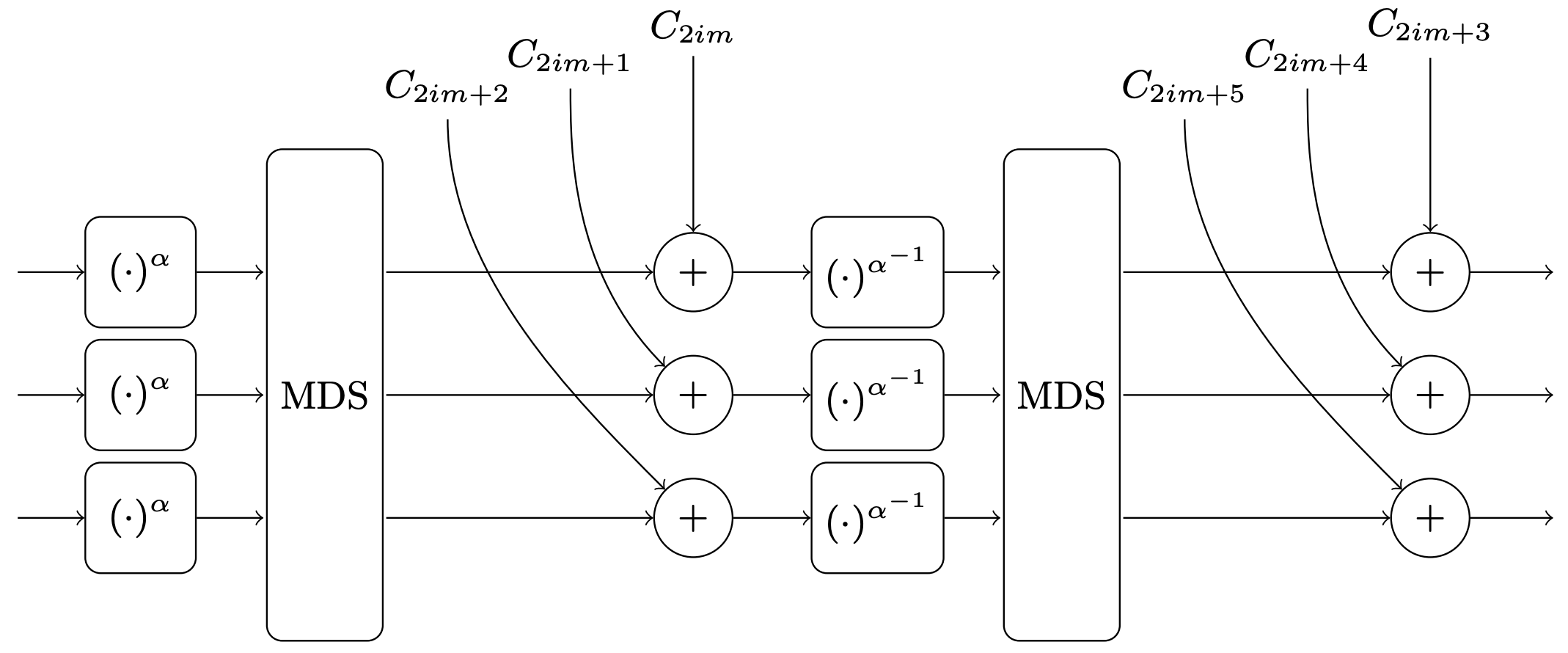
Fig. 2 Round \(i\) of the Rescue-XLIX permutation, with \(m=3\).#
Algorithm (The Rescue-XLIX permutation)
def rescue_XLIX_permutation ( parameters , state ) :
p , m , capacity , security_level , alpha , alphainv , N , MDS , round_constants = parameters
Fp = state [0 ,0].parent ()
for i in range ( N ) :
# S-box
for j in range ( m ) :
state [j ,0] = state [j ,0]^ alpha
# mds
state = MDS * state
# constants
for j in range ( m ) :
state [j ,0] += round_constants [ i *2* m + j ]
# inverse S-box
for j in range ( m ) :
state [j ,0] = state [j ,0]^ alphainv
# mds
state = MDS * state
# constants
for j in range ( m ) :
state [j ,0] += round_constants [ i *2* m + m + j ]
return state
a Python implementation
for r in range(self.N):
# forward half-round
# S-box
for i in range(self.m):
state[i] = state[i]^self.alpha
# matrix
temp = [self.field.zero() for i in range(self.m)]
for i in range(self.m):
for j in range(self.m):
temp[i] = temp[i] + self.MDS[i][j] * state[j]
# constants
state = [temp[i] + self.round_constants[2*r*self.m+i] for i in range(self.m)]
# backward half-round
# S-box
for i in range(self.m):
state[i] = state[i]^self.alphainv
# matrix
temp = [self.field.zero() for i in range(self.m)]
for i in range(self.m):
for j in range(self.m):
temp[i] = temp[i] + self.MDS[i][j] * state[j]
# constants
state = [temp[i] + self.round_constants[2*r*self.m+self.m+i] for i in range(self.m)]
